Понятие программной разработки библиотеки процедур в среде Maple

Пакет Maple состоит из быстрого ядра, написанного на Си и содержащего основные математические функции и команды, а также большого количества библиотек, расширяющих ее возможности в различных областях математики. Библиотеки скомпонованы из подпрограмм, написанных на собственном языке Maple, специально предназначенном для создания программ символьных вычислений. Наиболее интересные возможности системы Maple — редактирование и изменение этих подпрограмм, а также пополнение библиотек подпрограммами, разработанными для решения конкретных задач. Они уже появились в большом количестве, а лучшие из них вошли в Share-библиотеку пользователей, распространяемую вместе с пакетом Maple.

Программа уже превратилась в мощную вычислительную систему, позволяющую выполнять сложные алгебраические преобразования, в том числе над полем комплексных чисел, вычислять конечные и бесконечные суммы, произведения, пределы и интегралы, находить корни многочленов, решать аналитически и численно алгебраические (в том числе трансцендентные) системы уравнений и неравенств, а также системы обыкновенных дифференциальных уравнений и уравнений в частных производных. В Maple включены специализированные пакеты подпрограмм для решения задач аналитической геометрии, линейной и тензорной алгебры, теории чисел, комбинаторики, теории вероятностей и математической статистики, теории групп, численной аппроксимации и линейной оптимизации (симплекс-метод), финансовой математики, интегральных преобразований и т. п.

Создание новой библиотеки происходит следующим образом.

Прежде всего надо определить имя своей библиотеки, например mylib, и создать для нее на диске каталог (папку) с заданным именем. Процедуры в Maple ассоциируются с таблицами. Поэтому вначале надо задать таблицу-пустышку под будущие процедуры:

> restart;

> mylib:=tab1e():

mylib := table([])

Теперь надо ввести свои библиотечные процедуры. Они задаются с двойным именем — вначале указывается имя библиотеки, а затем в квадратных скобках имя процедуры. Для примера зададим три простые процедуры с именами fl, f2 и f3:

> mylib[fl]:=proc(x: Anything) sin(x)+cos(x) end:

> mylib[f2]:=proc(x:anything) sin(x)^2+cos(x)^2 end:

> mylib[f3]:=proc(x::anything) if x=0 then 1 else sin(x)/x fi end:

Рекомендуется тщательно проверить работу процедур, прежде чем записывать их на диск. Ограничимся, скажем, такими контрольными примерами:

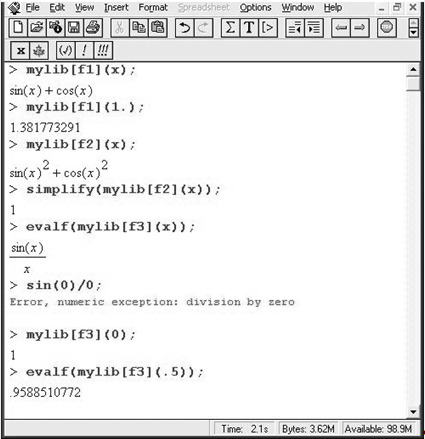
Можно построить графики введенных процедур-функций. Они представлены на С помощью функции with можно убедиться, что библиотека mylib действительно содержит только что введенные в нее процедуры. Их список должен появиться при обращении with (mylib):

> with(mylib);

[f1,f2,f3]

Теперь надо записать эту библиотеку под своим именем на диск с помощью команды save:

> save(mylib,`c:/ mylib.m);

Обратите особое внимание на правильное задание полного имени файла. Обычно применяемый для указания пути знак \ в строках Maple-языка используется как знак продолжения строки. Поэтому надо использовать либо двойной знак \\, либо знак /. В этом примере файл записан в корень диска С. Лучше поместить библиотечный файл в другую папку (например, в библиотеку, уже имеющуюся в составе системы), указан полный путь до нее.

После всего этого надо убедиться в том, что библиотечный файл записан. После этого можно сразу и считать его. Для этого вначале следует командой restart устранить ранее введенные определения процедур:

> restart;

С помощью команды with можно убедиться в том, что этих определений уже нет:

> with(mylib):

Error, (in pacman:-pexports) mylib is not a package

После этого командой read надо загрузить библиотечный файл:

> read('c:/mylib.m');

Имя файла надо указывать по правилам, указанным для команды save. Если все выполнено пунктуально, то команда with должна показать наличие в вашей библиотеке списка процедур fl, f2 и f3:

> with(mylib):

[f1. f2. f3]

И наконец, можно вновь опробовать работу процедур, которые теперь введены из загруженной библиотеки:

> fl(x):

sin(x) + cos(x) > simplify(f2(y});

Прочие статьи:

Связь педагогики с другими гуманитарными науками
Педагогика является самостоятельной наукой. Отделившись в свое время от философии, она не утратила тесной связи с другими гуманитарными науками: 1) философией; 2) психологией; 3) школьной гигиеной; 4) социологией; 5) фольклористикой и этнографией. Философия выполняет важную методологическую ...

Методы и приемы обучения аппликации в старшей группе
Основная задача обучения аппликации детей шестого года жизни - овладение разнообразными приемами вырезывания. На занятиях дошкольники изображают предметы, имеющие различные очертания, симметричные и несимметричные формы в статичном положении или с передачей несложного движения. Опираясь на предст ...

Стритбол шагает по планете
Стритбол – это выращенный из баскетбола отдельный вид спорта, а не просто уличный баскетбол, как было раньше. Креативность и шоу сочетаются с некоторыми баскетбольными правилами, переплетаясь с уличной культурой и хип-хопом. Самыми яркими и известными представителями стритбола является команда по ...

Меню сайта

• Главная
• Тест как объективное средство контроля
• Религиозное воспитание в семье
• Психологическая готовность ребёнка к школе
• Социализация и воспитание ребенка
• Виды и формы обучения
• Теория обучения
• Новая педагогика