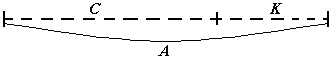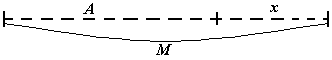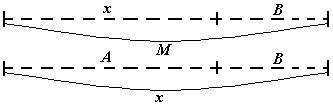Модель текста задачи как основа наглядно-образного мышления младших школьников
На уроке с помощью весов ученики устанавливают, что масса банки с водой и мешочка с песком одинакова. Затем дети записывают равенство масс с помощью отрезков равной величины. Обсуждая схему, дети приходят к выводу: величины необходимо обозначить, чтобы было понятно и другим людям. Учитель предлагает обозначить с помощью букв. Буквы подписываются и на предметах и на схеме (Рис.7).
Рис.7
Делается вывод, что о равенстве величин можно сказать формулой: А = Б. (Масса "А" равна массе "Б").
Итак, выполняя предметные действия (на основе измерения разных величин), отображая эти действия графически, сначала в виде рисунка, затем модели, учащиеся подходят к знаково-символической форме: равенству, уравнению.
В задании 60 дети знакомятся с понятиями "целое" и "части". Свои практические действия они переносят на бумагу с помощью схем.
В этой теме появляются текстовые задачи и уравнения, которые решаются с помощью, с опорой на схему. Работа со схемой в текстовых задачах является продолжением, а не новым материалом, как в традиционной системе, поэтому проходит легче, вызывая у детей интерес. Очень важно этот интерес у детей поддержать различными видами работ со схемой, которые помогли бы ребятам выбрать правильное решение задачи. Поэтому, на мой взгляд, необходимо, чтобы схему дети составляли сами, без помощи учителя. Составление схемы
К кормушке прилетело И синиц и К воробьев. Сколько всего птиц в кормушке?
На доске вычерчиваются все схемы, которые предлагают ребята. Каждая схема анализируется. После анализа остаются правильные, из которых выделяется более удобная для выбора решения (Рис.8).
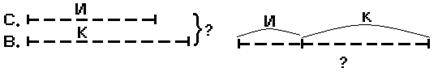
Рис.8
Из группы схем дети выбирают нужную (Рис.9).
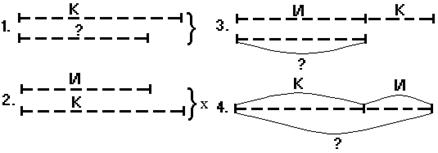
Рис.9
Выбрав схему 4, учащиеся объясняют решение задачи: все птицы – это целое, которое состоит из двух частей: воробьев и синиц, поэтому, чтобы найти, сколько всего птиц, нужно сложить К+И.
Анализируя после решения задачи схему 2, можно перейти к составлению уравнений:
х – И = К х = К + И
х – К = И х = И + К.
3. Активно проходит работа по составлению задач по схеме (Рис.10).
|
Рис.10 |
С + К = А, А – С = К А – К = С. |
С помощью схемы можно дать понятие обратной задачи. Дети решили задачу:" В кормушке было А воробьев, прилетели синицы и стало М птиц. Сколько птиц прилетело?" (см. Рис. 11).
|
Рис.11 |
A + x = M x = M – A. |
Затем схема меняется (Рис. 12).
|
Рис.12 |
x + B = M x = M – B x = A + B |
По схеме дети должны изменить условие задачи и уравнение к ней.
Во 2 – 4 классах работа над схемой продолжается. При решении составных задач схема помогает не только найти различные способы решения, но и выбрать самый рациональный, самый короткий. Например:"На трех полках стояло 116 книг. Когда с первой полки сняли 8 книг, со второй – 12 книг, а с третьей – 6 книг, на всех полках осталось поровну. Сколько книг стояло на первой полке первоначально?"
Прочие статьи:
Анализ существующих методик обучения младших
школьников программированию
Алгоритмизация как часть программирования является основным, центральным элементом содержания курса информатики. Однако объём её изучения ее остается дискуссионным, что связано как с важностью осуществления фундаментализации курса, так и с необходимостью проведения профориентации на профессию прог ...
Содержание и задачи сенсорного воспитания в современной отечественной
педагогике
Готовность ребенка к школьному обучению в значительной мере зависит от его сенсорного развития. Исследования, проведенные советскими психологами, показали, что значительная часть трудностей, возникающих перед детьми в ходе начального обучения (особенно в I классе), связана с недостаточной точность ...
Феномен детской игры
Игра относится к числу явлений, которые сопровождают человека на протяжении всей его жизни. Будучи многомерным и сложным феноменом, игра постоянно приковывает к себе внимание исследователей.
Эльконин Д.Б. отмечает в одной из статей, что игра имеет значение не только для тех процессов, которые в н ...
Меню сайта
- Главная
- Тест как объективное средство контроля
- Религиозное воспитание в семье
- Психологическая готовность ребёнка к школе
- Социализация и воспитание ребенка
- Виды и формы обучения
- Теория обучения
- Новая педагогика