Модель текста задачи как основа наглядно-образного мышления младших школьников

Чтобы самостоятельно решать задачи, ученик должен освоить различные виды моделей, научиться выбирать модель, соответствующую предложенной задаче, и переходить от одной модели к другой.

Необходимо отметить, что в данной работе я не касаюсь краткой записи условия задачи. Этот этап очень важен, однако, я исходила из того, что он традиционно присутствует в работе учителя. Поэтому главное внимание я уделяю тем приемам работы над задачей, которые в меньшей степени используются в традиционной системе, которые помогают мне пробудить у детей интерес к задаче, к поиску решений этой задачи.

При решении простых и составных задач на сложение и вычитание используется схематический чертеж.

Схематический чертеж прост для восприятия, так как:

· наглядно отражает каждый элемент отношения, что позволяет ему оставаться и при любых преобразованиях данного отношения;

· обеспечивает целостность восприятия задачи;

· позволяет увидеть сущность объекта в "чистом" виде без отвлечения на частные конкретные характеристики (числовые значения величин, яркие изображения и др.), что трудно сделать, используя другие графические модели;

· обладая свойствами предметной наглядности, конкретизирует абстрактные отношения, что нельзя увидеть, например, выполнив краткую запись задачи;

· обеспечивает поиск плана решения, что позволяет постоянно соотносить физическое (или графическое) и математическое действия.

Как было сказано выше, текстовые задачи на сложение-вычитание в 1-м классе строятся как частные случаи отношения величин, поэтому моделирование простой задачи у детей не вызывало затруднения, т.к. величины в задаче находятся в отношении целого и частей.

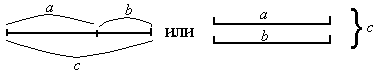
Рис.3 Схематический чертеж

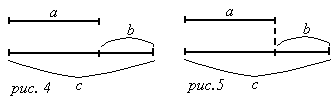
Если величины связаны отношением "больше (меньше) на" (Рис. 4.); Сравнение двух величин (Рис. 5.).

Освоение представлений графической, знаково-символической модели в 1-м классе.

Со схемами в системе Д.Б.Эльконина - В.В.Давыдова дети знакомятся с первых уроков, когда находят среди разных предметов одинаковые по какому-либо признаку: длине, площади, форме, объему.

Учащимся выдается набор полосок разных по длине, ширине и цвету. Их задача найти равные по какому-либо признаку. Сразу дети находят одинаковые по цвету, затем, путем наложения, одинаковые по длине. Перед учащимися ставится следующая задача:

Что нужно сделать, чтобы каждый раз не измерять полоски, а найти одинаковые сразу и быстро? Дети предлагают свои варианты: различные значки, но значки должны быть одинаковые, и на одинаковых полосках ставят значки.

А как записать в тетради, что среди полосок есть одинаковые?

Ребята обсуждают задание и приходят к выводу, что нужно зарисовать и поставить значки.

Далее дети выполняют более сложное задание: сравнивают сосуды по объему и находят равные. Равные сосуды необходимо запомнить, а лучше как-то отметить. Опять предлагаются значки.

Затем записывают в тетради с помощью рисунка и значка, что на столе есть одинаковые по объему сосуды.

После этого дети находят сосуды, одинаковые по другим признакам: материалу и высоте. Записывают в тетради, что сосуды равны по высоте с помощью вертикальных отрезков.

На последующих уроках дети с помощью схем учатся находить и определять равные и неравные величины показывать с помощью схем равенство и неравенство величин (Рис. 6).

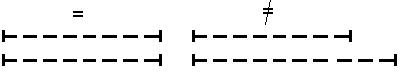
Рис.6

Через несколько уроков вводится буквенная символика. Все величины обозначаются буквами русского алфавита.

Прочие статьи:

Контроль и обратная связь: аспекты интеграции
Научная организация контроля является важнейшим условием эффективного управления процессом обучения иностранному языку. Специфика контролирующей деятельности заключается в том, что, взятая отдельно, она не формирует знания, умения, навыки, а дает необходимую для организации обучения «обратную инфо ...

Опора на учебник при разработке системы приёмов изучения материалов на уроке
В предыдущей главе была рассмотрена возможность подготовительной работы к уроку на основе учебника истории. Именно от этой подготовительной работы зависит урок, как главное звено в обучении учащихся. На уроке реализовывается педагогический замысел. Автор работы полностью согласен с авторами тех ра ...

Личностная характеристика «трудного» подростка
Жизнь подростка можно уместить в треугольник, углами которого будут семья, школа и улица (в самом широком понимании этого слова). С того момента, как ребенок начинает реагировать на социальные воздействия, он становится в какой-то степени зависимым от общества, тянется к нему и болезненно переноси ...

Меню сайта

• Главная
• Тест как объективное средство контроля
• Религиозное воспитание в семье
• Психологическая готовность ребёнка к школе
• Социализация и воспитание ребенка
• Виды и формы обучения
• Теория обучения
• Новая педагогика