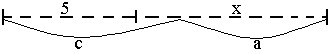Модель текста задачи как основа наглядно-образного мышления младших школьников

Строится схема (Рис. 13).

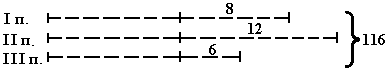
Рис.13

Дети анализируют задачу, а затем предлагают свой способ решения. Обычно средние и слабые ученики предлагают:

8 + 6 = 14 или 116 – 8 = 108

14 + 12 = 26 108 – 12 = 96

116 – 26 = 90 96 – 6 = 90

90 : 3 = 30 90 : 3 = 30

30 + 8 = 38 30 + 8 = 38

Сильные ученики предлагают свой вариант решения:

12 + 8 + 6 = 26

116 – 26 = 90

90 : 3 = 30

30 + 8 = 38

Все способы анализируются и выясняется, что все решили правильно. Выбирается самый рациональный. Те ребята, которые решили задачу рациональным способом, объясняют, что им помогло выбрать этот способ. (По схеме видно, что все книги состоят из 2-х частей, тех, что сняли и тех, которые остались на полках. Все книги, которые сняли – это целое. Целое состоит из 3-х частей, снимали с трех полок, а целое мы узнаем действием сложения, складываем все части).

При решении задач на умножение и деление первоначально использовали чертеж.

"В одной коробке 6 карандашей. Сколько карандашей в 3 таких коробках?"

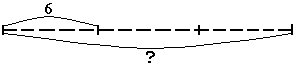
Рис.14

Использовался чертеж и при решении задач на пропорциональное деление. Например: "Одно число больше другого в 6 раз, а их сумма составляет 350. Найти числа."

Рис.15

При решении задач на движение в схему были сразу введены условные обозначения: S – сплошная дуга, V – стрелка, t – пунктирная дуга.

"Навстречу друг другу одновременно из двух деревень вышли две пешехода. Скорость одного из них 5 км/ч., а другого 4 км/ч. Через 2 час они встретились. Какое расстояние между деревнями?".

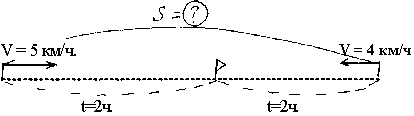
Рис.16

Четкие условные обозначение позволяют детям строить сложные схемы, видеть в них нужные формулы, отношения для решения задачи. Иногда мелочь в условных обозначениях, в схеме, позволяет не запутаться в числовых значениях составной задачи.

Так при решении задач на приведение к единице обозначение количества пунктирной дугой (на начальном этапе решения таких задач) позволило более четко представлять условие задачи и не путаться в числовых данных.

Ученики по чертежу устанавливают, что х – это часть. Чтобы найти часть, нужно из целого вычесть известную часть А.

И в 3 – 4 классе, когда изучаются свойства уравнения, схема снова приходит на помощь в проверке уравнений при доказательстве свойств.

Затем с помощью схемы проверяется: (Рис. 18).

Схемы помогают и при решении задач способом составления уравнения. С помощью схемы составляются уравнения к задачам.

При составлении уравнений к задачам, как и при решении задач на "приведение к единице", помогает краткая запись в виде таблицы. По таблице ребята находят равные величины или величины, которые можно уравнять.

Например: "За несколько пар коньков ценой 5000 руб. Заплатили 20.000рублей, а за столько же пар ботинок 96.000руб. Сколько стоила пара ботинок?"

Прочие статьи:

Последующее развитие устного метода и превращение его в планомерную систему
В опубликованных работах Гейнике содержится весьма мало сведений о методических и дидактических приемах работы по формированию словесной речи. В них имеются лишь отрывочные ссылки на практическую работу и нет завершенной картины описания его метода. От детально разработанного учебного процесса сох ...

Девиантные явления в жизни подростка
Как не различны формы девиантного поведения, они взаимосвязаны. Пьянство, употребление наркотиков, агрессивность и противоправное поведение образуют единый блок, так что вовлечение юноши в один вид девиантных действий повышает вероятность его вовлечение также и в другой. Противоправное поведение, ...

Нравственное воспитание старших дошкольников
Нравственное воспитание - это целенаправленный процесс формирования у подрастающего поколения высокого сознания, нравственных чувств и поведения в соответствии с идеалами и принципами коммунистической морали. Нравственное воспитание подрастающего поколения является объективной необходимостью, обу ...

Меню сайта

• Главная
• Тест как объективное средство контроля
• Религиозное воспитание в семье
• Психологическая готовность ребёнка к школе
• Социализация и воспитание ребенка
• Виды и формы обучения
• Теория обучения
• Новая педагогика